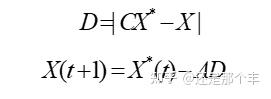优化方法·无约束非线性优化_红桃-红桃娱乐博客新闻站

摘要：就是求一个函数的最小值问题。并且计算机不适合用解析解。我们可以从一个初始点出发，一步一步走到期望的最优点，这就要求求出每一步往哪里走，走多长，从而把这种优化问题分解成求方向和求步长两个问题，求步长的时候，可以认为函

就是求一个函数的最小值问题。并且计算机不适合用解析解。

我们可以从一个初始点出发，一步一步走到期望的最优点，这就要求求出每一步往哪里走，走多长，从而把这种优化问题分解成求方向和求步长两个问题，求步长的时候，可以认为函数只有步长一个自变量，所以又称为一维搜索。

附上我写的如下一段代码：求方向可以选择4种算法之一，求步长则用的是不精确一维搜索方法一

%主函数集成了4种算法，所用的初始点可由用户自定义，用于求解无约束优化问题。
%目标函数定义在程序末尾的fun函数中，其梯度定义在gfun函数中，海塞矩阵（阻尼牛顿法需要）定义在d2fun函数中。
function Ti1
clear,clc;
x0=input('函数和梯度表达式在本程序末尾设置，现在请确定一个迭代初始点，以列向量表示：\
x0='); %用户可自定迭代初始点，增强了算法的灵活性
disp('请输入数字选择一种算法：1-最速下降法；2-阻尼牛顿法；3-共轭梯度法；4或其他输入-BFGS算法');
choice=input('选择...'); %choice是特定的选择变量，能够决定程序执行哪个算法
kmax=10000;   %最大迭代次数，避免算法无法收敛而一直进行
lambda=0;   k=0;    epsilon=1e-5;   g=gfun(x0); %不同的方法在迭代前都需要的参数，其中lambda是迭代步长，epsilon是精度
switch choice
    case 1
        disp('选择了最速下降法'); %提示选择的算法，下同
    case 2
        disp('选择了阻尼牛顿法');
        d2f=d2fun(x0); %阻尼牛顿法迭代前需要补充的参数，d2f即为海塞矩阵
    case 3
        disp('选择了共轭梯度法');
        n=length(x0);   s=zeros(n,1);   mu=0; %共轭梯度法迭代前需要补充的参数，mu是确定下个搜索方向最关键的参数μ
    otherwise
        disp('选择了BFGS算法');
        n=length(x0);   H=eye(n);   mu=0;   g=gfun(x0); %BFGS算法迭代前需要补充的参数，H和mu分别为公式中的Hk和μk
end
while(k<kmax)
    if(norm(g)<epsilon) %迭代停止准则
        break;
    end
    switch choice %根据选择的算法确定搜索方向
        case 1
            s=-g; %最速下降法的搜索方向
        case 2
            s=-inv(d2f)*g; %阻尼牛顿法的搜索方向
        case 3
            s=-g+mu*s; %共轭梯度法的搜索方向
        otherwise
            s=-H*g; %BFGS算法的搜索方向
    end
    %求步长采用不精确一维搜索算法一，相比直接求解驻点方程和精确一维搜索更简单，运算也更迅速
    c1=0.1;c2=0.5;a=0;b=inf;t=1;j=0;jmax=100; %一维搜索迭代参数设置
    %其中t为存储步长的变量，最大步数jmax的设置是避免一维搜索无法跳出循环而一直占用计算资源
    while(j<jmax)
        if(fun(x0)-fun(x0+t*s)+c1*t*(gfun(x0))'*s>=0) %采用Wolfe-Powell准则
            if((gfun(x0+t*s)-c2*gfun(x0))'*s>=0)
                break;
            else
                j=j+1;a=t;t=min(2*t,(t+b)/2);
            end
        else
            j=j+1;b=t;t=(t+a)/2;
        end
    end
    %以上为不精确一维搜索算法一过程
    lambda=t; %步长的确定
    x=x0+lambda*s; %下一个迭代点的确定
    %对最速下降法，已经可以进行下一步迭代，但对另外三种方法，需要更新参数
    switch choice
        case 1 %对最速下降法
            x0=x; %更新迭代点的值，下同
            g=gfun(x0); %求解新的梯度，下同
            k=k+1; %进行下一次迭代，下同
        case 2 %对阻尼牛顿法
            x0=x;
            g=gfun(x0);
            k=k+1;
            d2f=d2fun(x0); %阻尼牛顿法中海塞矩阵的更新
        case 3 %对共轭梯度法
            mu=norm(gfun(x))^2/(norm(g)^2); %共轭梯度法中μ的更新
            x0=x;
            g=gfun(x0);
            k=k+1;
        otherwise %对BFGS算法
            dx=x-x0;dg=gfun(x)-g;
            mu=1+(dg'*H*dg)/(dx'*dg); %BFGS算法中μ的更新
            H=H+(mu*(dx*dx')-H*dg*dx'-dx*dg'*H)/(dx'*dg); %BFGS算法中H的更新
            x0=x;
            g=gfun(x0);
            k=k+1;
    end
end
if(k==kmax) %迭代超过最大次数仍未收敛，说明选择的算法收敛性不好
    fprintf('算法在最大迭代次数，即%d步内仍未收敛\
',kmax)
    fprintf('最后一步迭代的取值点为(%.4f,%.4f)^T\
请检查无误后换用收敛性好的方法继续进行！\
',x0(1),x0(2))
else %迭代在有限的步数内正常收敛
    val=fun(x0);
    fprintf('算法进行了%d次迭代\
',k)
    fprintf('最终求得近似的最小值点为(%.4f,%.4f)^T\
',x0(1),x0(2)) %这里的输出样式适用于二元函数优化问题，n元函数相应扩充至x0(n)
    fprintf('近似的最小值为%.4f\
',val)
end

%n元函数f(x),请将每个自变量按x的分量形式输入，如x(1),x(2)。
function f=fun(x)
f=100*(x(2)-x(1)^2)^2+(x(1)-1)^2;

%f(x)的梯度，请将每个自变量按x的分量形式输入，如x(1),x(2)。
function gf=gfun(x)
gf=[ 2*x(1) - 400*x(1)*(- x(1)^2 + x(2)) - 2; - 200*x(1)^2 + 200*x(2)];

%f(x)的海塞矩阵，输入形式同上，下面的这个函数对阻尼牛顿法特别重要。
function d2f=d2fun(x)
d2f=[1200*x(1)^2 - 400*x(2) + 2,-400*x(1);-400*x(1),200];

通常的标准是使迭代中函数值逐渐减小，并且能收敛到极小点（思考：为什么不一定收敛到最小点？）

选择一个初始点（很重要，有的算法是局部收敛的），迭代法每一步都先求方向，后求步长，直到 $||\ abla f(\\bm x^{(k+1)})||\\leq\\varepsilon$ （连续函数最小值点通常梯度为0，即足够小）或其他条件

在掌握求方向和求步长的方法之前，应该先了解点列的收敛速度

有时迭代进行不下去了，前后两个点离得特别近，这时候也应该停止迭代，假如不是收敛到最优解，就应该换方法或者初值继续进行了

先来确定搜索方向，常用的方法可以选择：

最速下降法（又称梯度法）
阻尼Newton法（Newton法步长总为1，并入阻尼Newton法）
共轭梯度法（共轭方向法的一种）
DFP变尺度法（又称拟牛顿法，Huang类算法和自调节变尺度算法、BFGS变尺度算法是其变种，仅作了解）

最速下降法

直接取负导数方向作为搜索方向： $\\bm s^{(k)}=-\ abla f(\\bm x^{(k)})$
迭代收敛的条件是：

2.阻尼Newton法

取负海塞矩阵的逆×导数方向作为搜索方向： $\\bm s^{(k)}=-(\ abla^2 f(\\bm x^{(k)})^{-1}\ abla f(\\bm x^{(k)})$
至少是二阶收敛，收敛更快

缺点是函数必须二阶连续可微，海塞矩阵及其逆矩阵还是比较难求的
如果直接定步长为1，不停迭代，就是一般的Newton法，它要求初始点必须接近极小点，否者迭代可能不收敛

3.共轭梯度法

在掌握共轭梯度法之前，我们要了解A-共轭、A-共轭方向，而共轭梯度是生成共轭方向的一种方法

这种收敛很快，我们希望迭代过程中沿着共轭方向前进，并且这种方向在迭代过程中能够逐次形成，仍然需要利用上一个迭代点的梯度

调整搜索方向的公式可以写成 $设\\bm g^{(k)}=\ abla f(\\bm x^{(k)}),\\bm s^{(0)}=-\\bm g^{(0)}\\\\ 则\\bm s^{(k+1)}=-\\bm g^{(k)}+\\mu_{k+1,k}\\bm s^{(k)}\\\\ 式中\\mu_{k+1,k}=||\\bm g^{(k+1)}||^2/||\\bm g^{(k)}||^2\\\\$

4.DFP变尺度法

调整搜索方向的公式可以写成 $设\\bm g^{(k)}=\ abla f(\\bm x^{(k)}),\\bm s^{(0)}=-\\bm g^{(0)}\\\\ 则\\bm s^{(k+1)}=-\\bm H_{k+1}\\bm g^{(k+1)}\\\\ 式中\\bm H_{k+1}=\\bm H_{k}+\\dfrac{\\Delta \\bm x_{k}\\Delta \\bm x_{k}^{T}}{\\Delta \\bm x_{k}^{T}\\Delta \\bm g_{k}}-\\dfrac{\\bm H_{k}\\Delta \\bm g_{k}\\left(\\bm H_{k}\\Delta \\bm g_{k}\\right)^{T}}{\\Delta \\bm g_{k}^{T}\\bm H_{k}\\Delta \\bm g_{k}}\\\\\\Delta \\bm x_{k}=\\bm x_{k+1}-\\bm x_k,\\Delta \\bm g_{k}=\\bm g_{k+1}-\\bm g_k,\\bm H_0=\\bm I$

DFP算法是对称秩2算法，就是让 $\\mathrm{rank}\\bm C_k=2，即\\bm C_k=\\alpha_k\\bm{uu}^T+\\beta_k\\bm{vv}^T$

代入上面的式子，一些变量可以随便取，按下述取法就有了DFP的迭代公式：

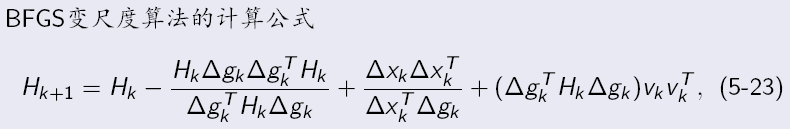
现在，搜索方向 $\\bm s$ 确定了，可以写出一个步长 $\\lambda$ 的函数 $f(\\bm x^{(k)}+\\bm s\\lambda)$ ，手算的话，求 $f'(\\lambda)=0$ 的值就能得到步长的最优值 $\\lambda^*$ ，然后 $\\bm x^{(k+1)}=\\bm x^{(k)}+\\bm s\\lambda^*$

但是用计算机没法算 $f'(\\lambda)=0$ ，这是一个符号表达式，必须用数值方法（ $|f'(\\lambda)|<\\varepsilon$ ）。计算机求步长的最优值所用的数值方法有：

1.精确一维搜索

2.不精确一维搜索：直接法和二次插值法

首先看精确一维搜索里使用导数的方法：

（一维）牛顿法

迭代公式是 $x_{k+1}=x_{k}-\\frac{f^{\\prime}\\left(x_{k}\\right)}{f^{\\prime \\prime}\\left(x_{k}\\right)}$ （思考：为什么有二阶导），最终使 $|f'(x_{k+1})|<\\varepsilon$ 的自变量值取为 $\\lambda^*$

平分法

其实就是解方程 $f'(\\lambda)=0$ 的二分法罢了：

三次插值法

$f(\\lambda)$ 的最小值在 $[a,b]$ 中，就利用两端点处的函数值和导数值构建三次插值样条函数（学过矩阵与数值计算就知道怎么办了），并以这个函数的极小值点作为 $\\lambda^*$

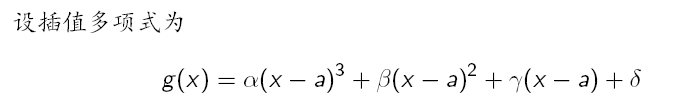
不用导数的方法有：

0.618法

成功-失败法

抛物线法

（I）（II）是保证区间足够小，（III）是保证拟合足够精确（充分接近原函数的极小值就行）

以上有的算法在开始前需要确定极小值所在的区间 $[a,b]$ ，可以用以下方法，作为了解：

最后是不精确一维搜索，不要求取 $f(\\lambda)$ 的极小值，而是下降到足够小即可：

上述可以写成Wolfe-Powell准则：

$f(\\bm x^{(k)})-f(\\bm x^{(k+1)})\\geq \\lambda_k c_1\\cdot (-\ abla f(\\bm x^{(k)})^T\\bm s^{(k)})\\\\ \ abla f(\\bm x^{(k+1)})^T\\bm s^{(k)}\\geq c_2\ abla f(\\bm x^{(k)})^T\\bm s^{(k)}$
式中常数满足 $0<c_1<c_2<1$ ，常取 $c_1=0.1,c_2=0.5$
记住这样两件事： $\ abla f(\\bm x^{(k)})^T\\bm s^{(k)}$ 是负的； $\\lambda_k$ 越大，第一个式子期望函数值的下降越大，而第二个式子通常和 $\\lambda_k$ 无关